The Cluster Editing problem (also referred to as the Correlation Clustering problem) is defined as follows:
Input: An undirected graph $G = (V, E)$.
Output: A set of edge modifications (addition or deletion) of minimum size that transforms $G$ into a cluster graph.
Recall that a cluster graph is a graph in which every connected component forms a clique; it is also characterized by the forbidden induced subgraph $P_3$ (a path on three vertices).
Example

In this example, one edge addition and two edge deletions transform the input graph into a cluster graph.
Background
Clustering plays an important role in modern society. Clustering is the task of partitioning instances into some number of groups (called clusters) such that instances in the same group are similar to one another. The Cluster Editing problem is one of the most natural ways to model clustering on graphs.
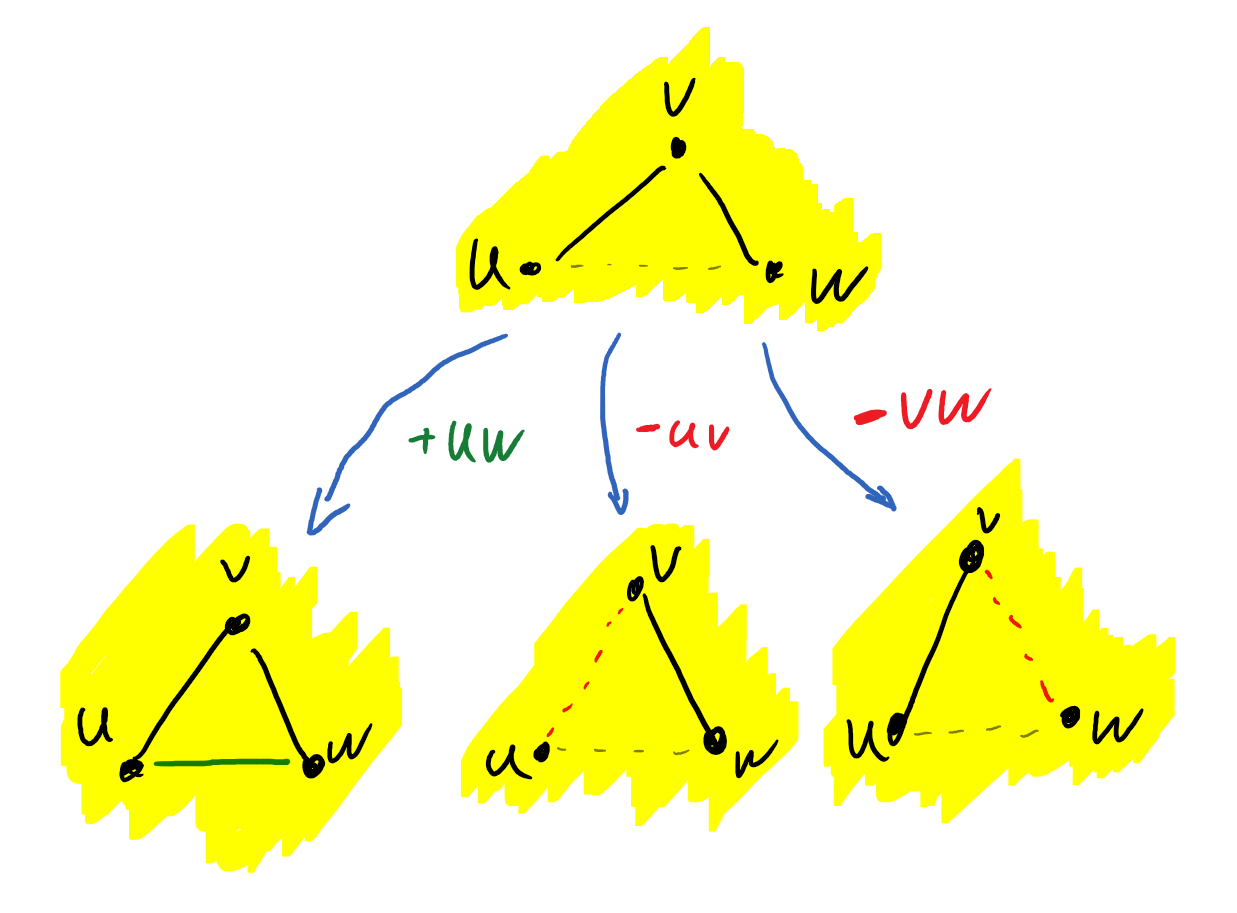
Cluster Editing is NP-hard but fixed parameter tractable (FPT) for the minimum solution size $k$. In fact, there is a simple $O(3^k \cdot (|V| + |E|))$-time branching algorithm. If there is an induced path $(u, v, w)$ on three vertices (which can be found in linear time), we branch into three cases: add an edge $uw$, delete the edge $uv$, or delete the edge $vw$.
Literature
- van Bevern, R., Froese, V. and Komusiewicz, C., 2018. Parameterizing edge modification problems above lower bounds. Theory of Computing Systems, 62(3), pp.739-770.
- Böcker, S., 2012. A golden ratio parameterized algorithm for cluster editing. Journal of Discrete Algorithms, 16, pp.79-89.
- Böcker, S. and Baumbach, J., 2013. Cluster editing. In Conference on Computability in Europe, pp. 33-44.
- Cao, Y. and Chen, J., 2012. Cluster editing: Kernelization based on edge cuts. Algorithmica, 64(1), pp.152-169.
- Fomin, F.V., Kratsch, S., Pilipczuk, M., Pilipczuk, M. and Villanger, Y., 2014. Tight bounds for parameterized complexity of cluster editing with a small number of clusters. Journal of Computer and System Sciences, 80(7), pp.1430-1447.
