The Directed Feedback Vertex Set Problem is defined as follows:
Input: A directed graph $G = (V, E)$.
Output: Find a minimum subset $X \subseteq V$ such that, when all vertices of $X$ and their adjacent edges are deleted from $G$, the remainder is acyclic.
Thus a feedback vertex set of a graph is a set of vertices whose deletion leaves a graph acyclic.
Example
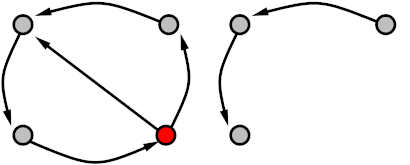
In this example, deleting/removing the red vertex and its edges in the left graph results in the graph on the right hand side and leaves the remaining graph without any cycles.
Background
The Directed Feedback Vertex Set Problem has a wide range of applications including deadlock detection, program verification and VLSI chip design. The problem is NP-complete even if restricted to graphs with maximum in- and out-degree two. The optimization problem can be solved in $O^*(1.9977^n)$ due to an algorithm by Razgon. Chen et al. have shown that the problem is fixed-parameter tractable if parameterized with the solution size $k$, i.e. Chen et al. develop an algorithm with running time $4^kk!n^{O(1)}$. Note that the problem is equivalent to the edge-deletion variant commonly called Feedback Arc Set: there are reductions in both ways that preserve the value of the optimal solution and only blow up the size of the graph (sum of vertices and edges) by a polynomial factor.
Literature
- Cygan, Marek; Fomin, Fedor V.; Kowalik, Lukasz; Lokshtanov, Daniel; Marx, Daniel; Pilipczuk, Marcin; Pilipczuk, Michal; Saurabh, Saket (2015), “Parameterized Algorithms”, Chapter 8.6, Springer.
- Karp, Richard M. (1972), “Reducibility Among Combinatorial Problems”, Proc. Symposium on Complexity of Computer Computations, IBM Thomas J. Watson Res. Center, Yorktown Heights, N.Y., New York: Plenum, pp. 85–103
- Razgon, I. (2007), “Computing minimum directed feedback vertex set in $O^*(1.9977^n)$”, in Proceedings of the 10th Italian Conference on Theoretical Computer Science, World Scientific, pp. 70–81
- Chen, Jianer; Liu, Yang; Lu, Songjian; O’Sullivan, Barry; Razgon, Igor (2008), “A fixed-parameter algorithm for the directed feedback vertex set problem”, Journal of the ACM, 55 (5), Art. 21
- Fleischer, Rudolf, Xi Wu, and Liwei Yuan. “Experimental study of FPT algorithms for the directed feedback vertex set problem.” European Symposium on Algorithms. Springer, Berlin, Heidelberg, 2009.
