PACE 2025 - Dominating Set

Dominating Set

The first challenge for this year is Dominating Set:

Input: An undirected graph $G$
Output: A dominating set for $G$

What is a dominating set?

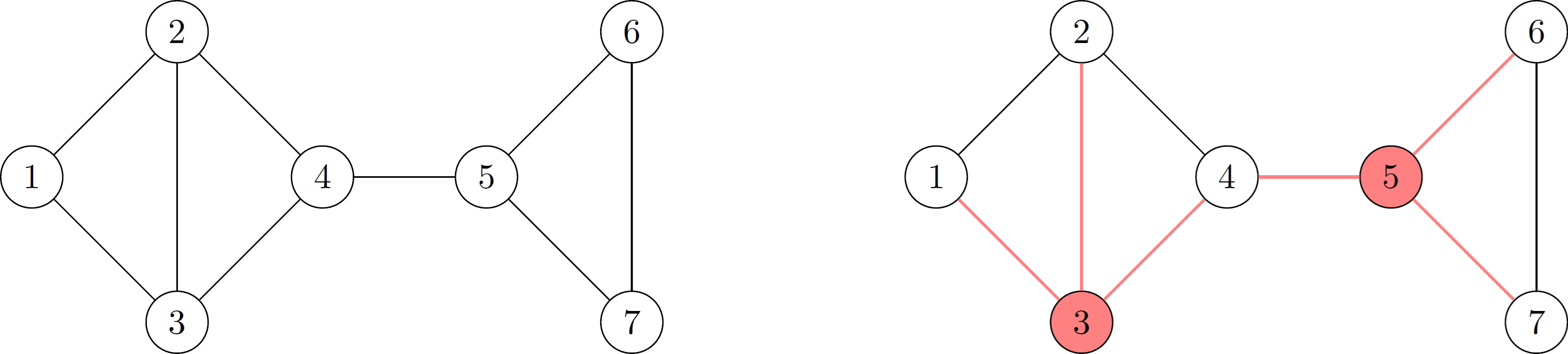
A dominating set for a graph $G$ is a set $D \subseteq V(G)$ such that every vertex or one of its neighbors is contained in $D$, that is, for all $v \in V(G)$ we have $v \in D$ or there is $u \in D$ with $uv \in E(G)$.

Example

Complexity

Dominating set is known to be NP-complete, even on planar graphs of maximum degree $3$. The problem is also W$[2]$-hard (parameterized by solution size), and hence believed to be not fixed-parameter tractable (fpt) in general. However, it is fpt on many structurally restricted classes of graphs, e.g. planar graphs, degenerate graphs, biclique-free graphs, and more. The problem is linear time solvable on all graphs with a fixed bounded treewidth or cliquewidth.

A simple greedy algorithm on $n$-vertex graphs yields an $\ln n$ approximation, and it is NP-complete to compute better approximations in general. On several restricted graph classes we can compute much better approximations. For instance, the problem admits a polynomial-time approximation scheme (PTAS) on planar graphs and, more generally, on graph classes with subexponential expansion. It admits a constant factor approximation on classes of bounded degeneracy and an $O(d\cdot \ln k)$ approximation (where $k$ denotes the size of a minimum dominating set) on classes of VC dimension $d$.

Verifier and test set

A verifier with a small test set is now available on Github.

Tracks

Exact Track

The task is to compute an optimal solution for each given graph, that is, a minimum dominating set. For each instance, the solver has to output a solution within a time limit of 30 minutes and a memory limit of 8 GB.

Instances in this track will satisfy structural properties that theoretically allow the efficient solution of the problem, e.g. be planar and have a moderately small domination number, have moderately small treewidth or cliquewidth, etc.

Submissions should be based on provably optimal algorithms. With the solver we ask for a sketch of correctness. Submissions that output an incorrect solution or a solution that is known to be non-optimal will be disqualified. Besides dedicated algorithms, we also encourage submissions based on other paradigms such as SAT, MaxSAT, or ILPs. We allow the use of open source SAT solvers and ILP solvers.

Heuristic Track

In this track, the solver shall compute a good solution quickly. The solver will be run on each instance for 5 minutes and a memory limit of 8GB. After 5 minutes the solver receives the Unix signal SIGTERM. When receiving this signal, the process has to output a dominating set to the standard output and terminate. If the program does not halt in a reasonable time after reserving the signal, it will be stopped via SIGKILL. In this case the instance is counted as time limit exceeded.

For this track solutions do not have to be optimal. However, solvers that produce an incorrect solution will be disqualified.

Final Evaluation

The final score will be computed over a set of 100 private instances that are similar to the 100 public instances.

Input and Output

Input Format

We use the standard DIMACS-like .gr format for graphs.

Lines are separated by \n. Lines starting with a c are considered to be a comment and hence ignored. The first (non-comment) line starts with a p followed by a problem descriptor, which is ds for the Dominating Set problem, followed by the number of vertices n and number of edges m. The vertices are numbered from 1 to n. Every other line contains two numbers representing an edge. Hence, the total file consists of $m+1$ non-comment lines. The example graph above can be described by the following file.

    c I am a comment
    p ds 7 9
    1 2
    1 3
    2 3
    2 4
    3 4
    4 5
    5 6
    5 7
    6 7

Output Format

The output format is similar, the main difference being that each line consists of a single number (representing a vertex of the solution instead of an edge). We expect the first non-comment line to be a number representing the size of your solution. Every other (non-comment) line is expected to be a single number, representing a vertex of the solution. Hence, the total file consists of $k+1$ non-comment lines, where $k$ is your solution size. The solution in the example above can be specified by the following output.

    c The first non-comment line represents the solution size
    2
    3
    5

Literature