PACE 2021 - Track Details

For PACE 2021, we offer the following three tracks:

Exact Track
Heuristic Track
Kernelization Track

You can participate in any subset of the three tracks. In each tack we use this input format.

Exact Track

Your submission should find an optimal cluster editing (a set of edge modifications that turns the input graph into a cluster graph; see also the problem description) within 30 minutes. We expect your submission to be an exact algorithm, although we do not ask you to provide a proof of it. If for some instance your program returns a solution that is not optimal within the time limit, your submission will be disqualified. Moreover, if the output of your program for any instance turns out to be not a cluster editing, your submission will be disqualified as well. See also the input format and output format.

Ranking method: You will be ranked by the number of solved instances. In case of a tie, the winner is determined by the time required to solve all instances.

Heuristic Track

Your submission should find a cluster editing (a set of edge modifications that turns the input graph into a cluster graph; see also the problem description) within 10 minutes. See also the input format and output format.

Termination: Your program will receive the Unix signal SIGTERM on timeout. When your process receives this signal, it must immediately print the current best solution to the standard output and then halt. You can find examples how to handle SIGTERM in several popular programming languages. If the process blocks for too long, say 30 seconds after the initial SIGTERM signal, we will forcefully stop it with SIGKILL.

Ranking method: You will be ranked by the average over all instances of 100 × (best solution size) / (solution size). Here, (solution size) is the size of the solution returned by your submission and (best solution size) is the size of the smallest solution known to the PC committee (which may not be optimal). If the output of your program turns out to be not a cluster editing (or there is no output on SIGKILL) for some instance, (solution size) for the instance will be regarded as infinity (so you will receive no point).

Kernelization Track

Our goal for this track is to develop efficient and effective preprocessing software that can be combined with exact or heuristic algorithms (see also discussion). Your submission should return a smaller “equivalent instance” to the one given as input within 5 minutes. Moreover, your submission should contain a “solution-lifting algorithm” that efficiently computes a solution for the input graph given a (not necessarily optimal) solution for the equivalent instance constructed by your submission.

More precisely, for an input graph $G$, your submission has to return a number $d$ and a graph $G’$ such that $\mathrm{opt}(G) = \mathrm{opt}(G’) + d$, where $\mathrm{opt}(H)$ denotes the minimum number of edge modifications to required to turn $H$ into a cluster graph (cf. see also the problem description) for the graph $H$.

Submission to optil.io: Since two programs cannot be verified together on optil.io, we use the following adjusted requirements (only for optil.io, not final submission). We provide four heuristics (see below for explanations and source code for these heuristics). Your submission has to use these heuristics to compute cluster editing sets $S_1’, …, S_4’$ for $G’$. From these solutions $S_1’, …, S_4’$, your submission has to compute solutions $S_1, …, S_4$ for $G$ such that $|S_i| \le |S_i’| + d$ for each $i = 1, \dots, 4$. Your submission will be disqualified if $\mathrm{opt}(G) \ne \mathrm{opt}(G’) + d$, $S_i$ is not correct, or $|S_i| > |S_i’| + d$ for any $i = 1, \dots, 4$. It is unfortunately impossible to verify $\mathrm{opt}(G) = \mathrm{opt}(G’) + d$ on optil.io, since it requires an optimal solution for a Cluster Editing instance constructed by your submission. Rather, any submission will be accepted as long as $S_i$ is a cluster editing with $|S_i| \le |S_i’| + d$. Thus, participants need to ensure $\mathrm{opt}(G) = \mathrm{opt}(G’) + d$ on their own machine. Final submission detected to violate this requirement will be disqualified.

Heuristics:

Delete all edges.
Insert all nonedgpes. (Together with heuristic 1 this ensures that no edge is handled equally in all heuristics.)
Greedy: Take vertex $v$ with smallest name (vertices are named $1$ to $n$), make $N[v]$ a clique in the resulting cluster graph. Delete $N[v]$ from the graph and repeat until the graph is empty.
Same as 3 but with $v$ being the vertex with the largest name.

Output Format: The first line contains a single number $d$. The following lines contain the output graph $G’ = (V’, E’)$, which has be given in the same way as the input, i.e., the second line contains p cep followed by the number $n$ of vertices and $m$ edges (separated by a whitespace) and the subsequent $m$ lines contain a list of edges where each line consists of two integers in the range $1$ to $n$. See the input format for the details. Then, $S_1, \dots S_4$ must be given in this order. The first line for $S_i$ contains $|S_i|$. For the following $|S_i|$ lines are in the form i j followed by the new line character \n, where i j represents an edge modification. Here is a dummy example.

Final submission: In the source code submitted to EasyChair, the output should only contain the first $|E’| + 2$ lines, i.e. the lines for $S_1, \dots S_4$ should be excluded. Your output may contain comment lines, starting with the character c. Note that a “solution-lifting algorithm” must be included as well. The input for “solution-lifting algorithm” has three parts:

The input graph (see Input Format)
The output of your kernelization (see above).
A heuristic solution $S’$ for the kernel (every line is in the form i j followed by the new line character \n, where i j represents an edge modification).

There are two lines consisting of # to indicate the end of first part and second part. Here is an example.

p cep 3 2
1 2
2 3
#
1
p cep 2 1
1 2
#
1 2

Your “solution-lifting algorithm” needs to compute a solution $S$ for the input graph with $|S| \le |S’| + d$. For the output, use the same format as Exact Track and Heuristic Track.

Ranking method: You will be ranked by the average over all instances of 100 × (best points) / (your points). Here, (your points) is $(|V’| + |E’| + 1) / (d + 1)$, where $(V’, E’)$ is the graph returned by your submission and (best points) is the smallest points among all submissions. Note that +1 in (your points) is included to avoid division by 0.

(March 26th: Ranking method has been updated.)

Input Format

The input graph is given via the standard input, which follows the DIMACS-like .gr file format described below.

Lines are separated by the character \n. Each line that starts with the character c is considered to be a comment line. The first non-comment line must be a line starting with p followed by the problem descriptor cep and the number of vertices n and edges m (separated by a single space each time). No other line may start with p. Every other line represents an edge, and must consist of two decimal integers from 1 to n separated by a space; moreover, graphs are considered to be undirected. Multiple edges and loops are forbidden. For example, a path with four edges can be defined as follows:

c This file describes a path with five vertices and four edges.
p cep 5 4
1 2
2 3
c we are half-way done with the instance definition.
3 4
4 5

Output Format for Exact Track and Heuristic Track

Every line must in the form i j followed by the new line character \n, where i j represents an edge modification. Here’s some example:

Use this to verify whether the output is a cluster editing. To compile this verifier for Cluster Editing execute make all in the command line. Afterwards, there is an executable verifier. The verifier takes two arguments: paths to an input graph file and a solution file containing a list of edges. It checks whether the graph is a cluster graph after the edge modifications in the solution file are made. Note that it does not check for optimality.

Benchmark for Exact Track and Kernelization Track

We use the same benchmark instances for evaluating Exact Track and Kernelization Track. There are 200 instances, labeled exact001.gr to exact200.gr. The instances are ordered lexicographically by non-decreasing $(n,m)$ where $n$ is the number of vertices and $m$ is the number of edges. The odd instances are public and the even instances are private. Instances exact001.gr to exact157.gr have graph size ($n + m$) at most 10,000. The largest instance does not exceed size 200,000. For every instance, the number of vertices is at most 700. See below for the distribution of instance sizes.

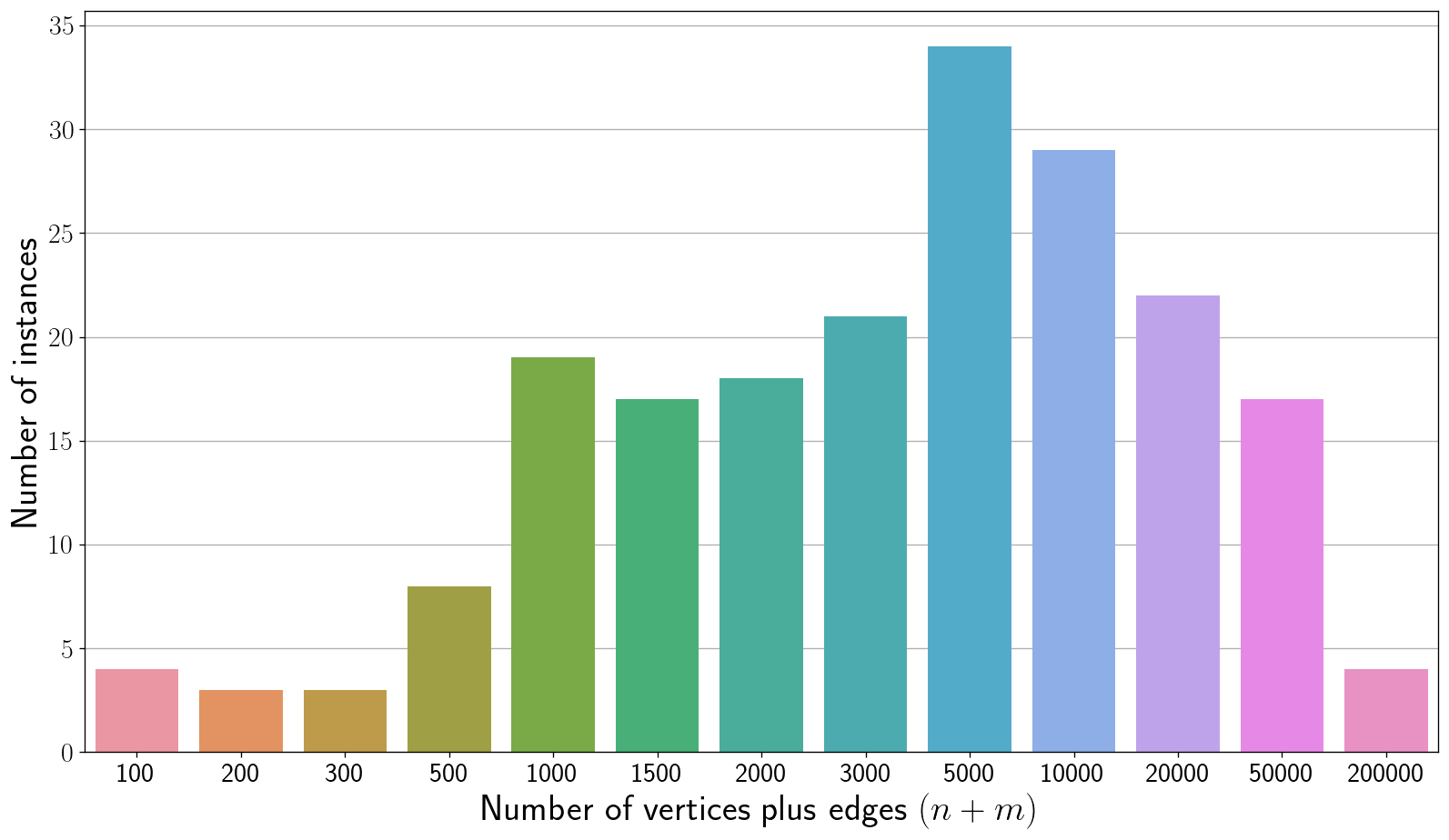
exact

Download the instances here.

Benchmark for Heuristic Track

There are 200 instances, labeled heur001.gr to heur200.gr. The instances are ordered lexicographically by non-decreasing $(n,m)$ where $n$ is the number of vertices and $m$ is the number of edges. The odd instances are public and the even instances are private. Instances heur001.gr to heur170.gr have graph size ($n + m$) at most one million. The largest instance does not exceed size five million. For every instance, the number of vertices is at most two million and there are at least 100 instances in which the number of vertices is at most 1,000. See below for the distribution of instance sizes.

heur

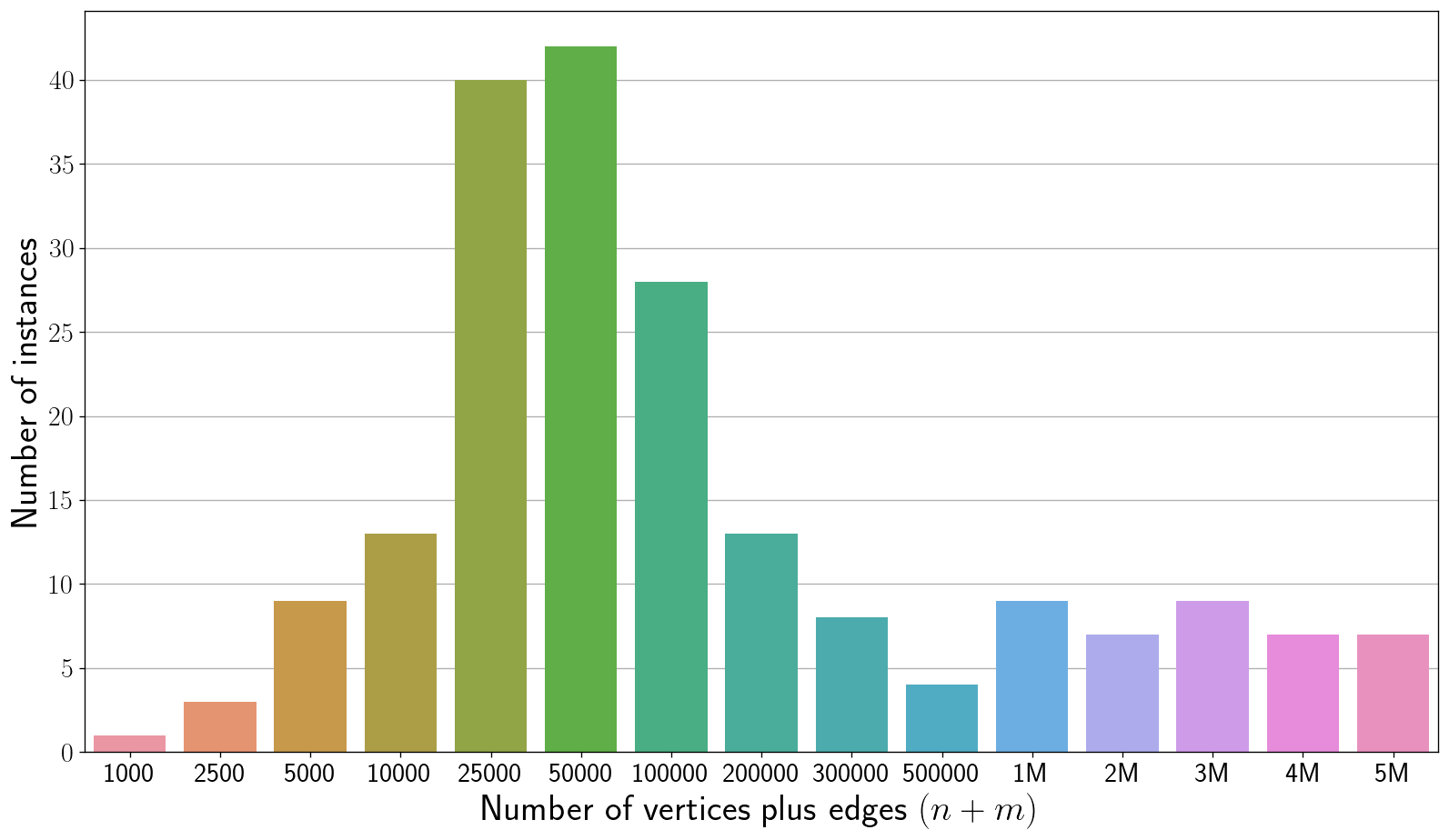
Download the instances here.

Appendix: Discussion on Kernelization Track

Kernelization is an important and vibrant field within parameterized algorithmics (see also a recent book on kernelization). Formally, kernelization is defined for decision problems: A kernelization algorithm (or kernel for short) is a polynomial-time algorithm that, given an instance $(G, k)$ of Cluster Editing, returns an equivalent Cluster Editing instance $(G’, k’)$ such that $k’ \le f(k)$ for some computable function $f$. Here, two instances $(G,k)$ and $(G’,k’)$ are said to be equivalent if $(G,k)$ is a yes-instance $\iff$ $(G’,k’)$ is a yes-instance.

Note that there are a list of issues appearing when we want to apply this concept in practice or in a programming contest:

For many problems (including Cluster Editing) the standard parameter $k$ (solution size) is not known in advance.
Instead of knowing the value of an optimal solution the task is usually to compute such a solution.

The solution to issue 1 is relatively easy (and probably undisputed): For an input graph $G$ one returns a number $d$ and a graph $G’$ such that $\mathrm{opt}(G) = \mathrm{opt}(G’) + d$. Our solution for the other issue is probably a bit controversial (if you have better ideas, please contact us). To address issue 2, we added the requirement that any submission has to be able to create a solution for the input graph given a (not necessarily optimal) solution for the returned kernel. Thus, we make the kernelization algorithms of the submissions attractive for people who would like to solve Cluster Editing in practice: the kernelization algorithms can be combined with any other solver computing some cluster editing set without much overhead work. However, we realize that this is an additional requirement on the submission, thus increasing the bar for entering the contest. Moreover, we might exclude existing kernelization algorithms that can only work with optimal solutions. Overall, we hope that our decision will make our beautiful (and so far very theoretical) kernelization community more accessible to the more practical communities.