PACE 2026: Format specification

Input format

Each instance consists of a single text with different line types:

• Empty lines carry no strict meaning and can be ignored.
• Lines starting with the symbol #. They can always be ignored, but may contain useful data. The meaning of these lines is determined by the second character:
  • #p {t} {n} indicates that the file contains $t$ trees with $n$ leaves each. This line appears before the first Newick line (see below).
  • #x {parameter-key} {value} contains a precomputed instance parameter (see Parameters below). The value is formatted in a JSON subset, such that parsing should be easy, even if your language does not support a fully fledged JSON parser.
  • #s {key} {value} is reserved for the official tools. Solvers may not use these values.
  • # is a comment line.
• All other non-empty lines contain a tree description in the Newick format (see below) and represent an input tree. There are exactly $t$ such lines.

Files do not contain unnecessary whitespace anywhere (e.g., Newick or JSON expressions contain no (unnecessary) whitespaces, lines do not start or end with a whitespace, …).

Relevant subset of the Newick format

We use a subset of the standard Newick format for phylogenetic trees: Each tree is represented by a valid parenthesis-expression in a dedicated line. The whole expression is terminated with a semicolon. It is defined recursively:

• Each leaf is represented by its label, a positive integer from $1, 2, …, n$ where $n$ is the number of leaves indicated in the #p line.
• Each internal node has exactly two children and no own label. It is denoted as (A,B) where A and B are the expressions of the two children. The order of children does not carry meaning (other than definining the indices of inner nodes), i.e. (A,B) and (B,A) imply the same tree.

Each leaf label $1, 2, …, n$ appears exactly once per Newick expression.

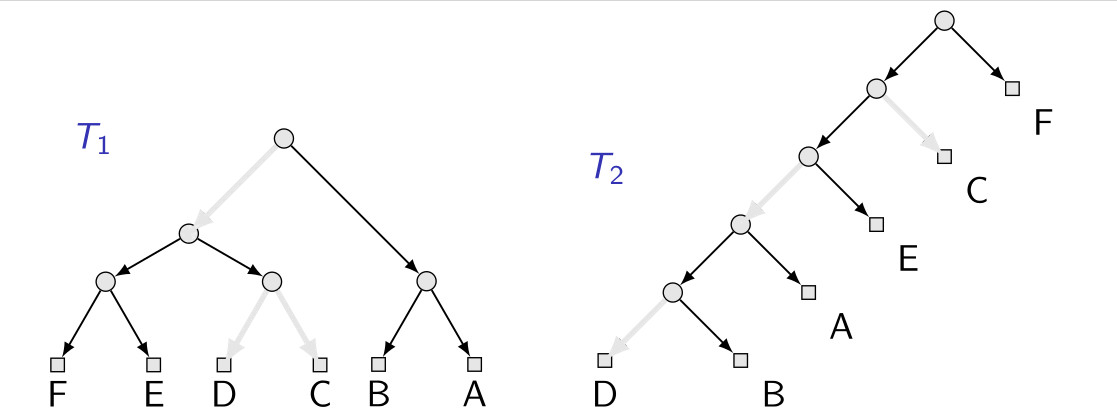
The two trees in the example above can be represented as follows:

#p 2 6
(((5,6),(3,4)),(1,2));
(((((4,2),1),5),3),6);

But it may also contain comments:

# This is a demo file consisting of two trees with 6 leaves each:
#p 2 6
# It may have comments here, ...
(((5,6),(3,4)),(1,2));
# ... or here ...

(((((4,2),1),5),3),6);
# ... or even here ...
#x height [2,5]

Output format

The output format is the same as the input format, but consisting of $k$ phylogenetic trees whose leaf labels are a partition of the leaf labels of each input tree. Empty lines and lines starting with # are ignored.

The solution for the example above could be the following:

# internal debugging message 1
# the following line could --equivanlently-- be: (5,6);
(6,5);
4;
# internal debugging message 2
3;
(1,2);

Parameters

We add a selection of heuristicially computed parameter approximations including their certificates (if applicable). Each parameter is computed with a limited time budget (at most 30s); if no solution could be obtained within the predetermined time budget, we omit the parameter from the instance.

Each parameter is provided in its own line and only after the last Newick line (i.e., if a solver does not use parameters, it can stop parsing the input). A line is formated as #x {parameter-key} {value} where {value} is a JSON formatted expression.

Indices of inner nodes

Parameters may reference inner nodes. Here we use the following convention: the root of the $i$-th tree ($i \ge 1$) has index $i(n - 1) + 2$. The remaining inner nodes follow in preorder. This choice conviently coincides with the Newick format: An inner node has index $j = i(n - 1) + 1 + b$ iff it is represented by the $b$-th ($b \ge 1$) opening bracket in the $i$-th Newick line.

Tree decomposition of display graph: treedecomp

An undirected display graph of forest $F$ with trees $T_1, \ldots, T_t$ can be obtained by merging all leaves with the same label and replacing directed edges with undirected ones. The parameter treedecomp is a tree decomposition of small treewidth. It is provided in the format #x treedecomp [{tw},{bags},{edges}] where

• {tw} is the treewidth of the provided tree decomposition, i.e. the largest bag has size {tw} + 1. This may or may not minimal.
• bags is a list of bags, each containing nodes where the indices ${1, \ldots, n}$ are leaf labels and all remaining refer to inner nodes.
• edges are edges between bags; the first bag has index $1$.

#x treedecomp [2,[[8,16],[8,11,16],[1,11,15],[2,11,16],[7,8,11],[8,10,16],[3,10,13],[4,10,16],[8,9],[5,9,14],[6,9,12]],[[1,2],[1,6],[1,9],[2,3],[2,4],[2,5],[6,7],[6,8],[9,10],[9,11]]]

Your favorite parameter is missing?

We strongly encourage participants to propose additional parameters via Zulip! Each proposal should reference a publically available solver.