PACE 2026 - (rooted) Maximum-Agreement Forest

Maximum-Agreement Forest

The challenge problem for this year is (rooted) Maximum-Agreement Forest:

Input: A list of phylogenetic trees on the same leaf-set $X$
Output: An agreement forest for all input trees with a minimum number of trees

What is a phylogenetic tree?

A phylogenetic tree $T$ is a tree whose edges are directed away from the unique root. Its sinks/leaves (vertices with out-degree zero) are bijectively labelled with a set $X$ (for simplicity, it is often assumed that $X$ is the set of leaves of $T$).

What is an agreement-forest?

An agreement forest for a set of trees $T_1$, $T_2$, $\ldots$ on the same set $X$ of leaves (leaf-labels) is a forest $F$ of phylogenetic trees whose leaf-set is $X$ such that $F$ can be obtained from each $T_i$ by first removing directed edges and then exhaustively contracting vertices that are not in $X$ but have in- and out-degree at most one (“cleanup”).

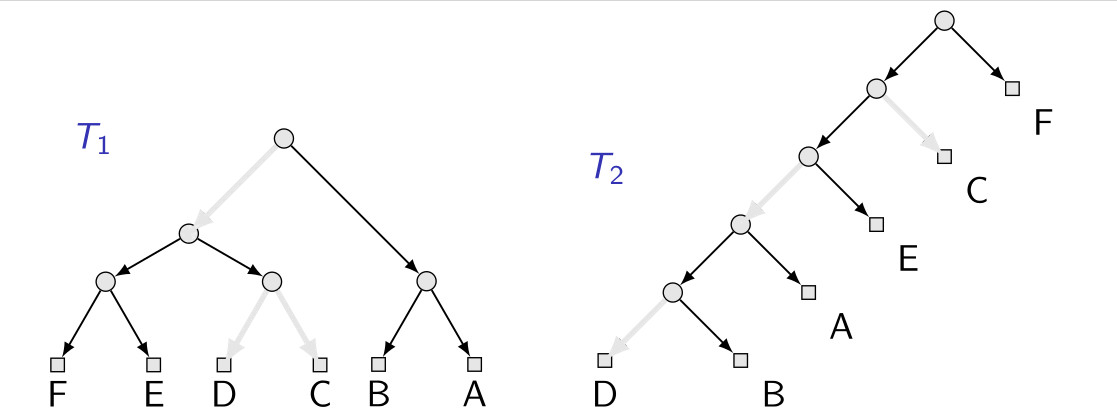
Example

It is worth to note that a maximum-agreement forest for two phylogenetic trees $T_1$ and $T_2$ contains exactly one more tree than the so-called “rooted subtree prune and regraft” (SPR) distance between $T_1$ and $T_2$. Formally, the distance is defined as the smallest number of “SPR-moves” necessary to turn $T_1$ into $T_2$ (or vice versa – the distance is a metric), where an SPR-move consist of removing any edge $uv$, subdividing any edge $xy$ of the weak component of $u$ with a new vertex $z$, contracting $u$ and adding the edge $zv$. Results for computing the rooted SPR-distance are often applicable for computing MAFs for two trees.

Complexity

Deciding whether two rooted binary trees on $n$ leaves have an agreement forest with $k$ trees is known to be NP-complete. However, this problem can be solved in $O^\star(2.35^k)$ time and there is a kernel with $28k$ leaves. It also admits a polynomial-time 2-approximation algorithm. If the input consists of $t>2$ trees, then the problem can be solved in $O(3^knt)$ time or $O^\star(2.42^kn^4t^3)$ time. Structural parameters have not been explored for either case.

Verifier and test set

A verifier with a small test set will be made available.

Public instances

Public instances will be made available.

Tracks

Exact Track

The task is to compute an optimal agreement forest for the given phylogenetic trees. For each instance, the solver has to output a solution within a time limit of $x$ minutes and a memory limit of $y$ GB ($x$ and $y$ to be determined).

Instances in this track will come with precomputed parameter values and proofs (i.e. decompositions of certain width). We will take requests for parameters to be included in this list.

Submissions should be based on provably optimal algorithms. Submissions that output an incorrect solution or a solution that is known to be non-optimal will be disqualified. Besides dedicated algorithms, we also encourage submissions based on other paradigms such as SAT, MaxSAT, or ILPs. We allow the use of non-commercial SAT solvers and ILP solvers provided they are not subject to licenses that restrict the free distribution of your solvers.

Heuristic Track

In this track, the solver shall compute a good solution quickly. The solver will be run on each instance for a short time with limited memory. After this time, the solver receives the Unix signal SIGTERM. When receiving this signal, the process has to output a solution to the standard output and terminate. If the program does not halt in a reasonable time after receiving the signal, it will be stopped via SIGKILL. In this case, the instance is counted as “time limit exceeded”.

For this track, solutions do not have to be optimal. However, solvers that produce an incorrect solution will still be disqualified.

Lower-Bound Track

The goal of this track is to encourage research on good lower bounds. The idea is that good lower bound allow solvers to determine early that a solution is “good enough” to be within some radius of the optimum. Only solutions within a fixed radius will be considered valid and valid solutions will be scored by their running time.

Final Evaluation

The final score will be computed over a set of $x$ private instances that are similar to the public instances.

Input and Output

Input Format

We use the standard [Newick format] for phylogenetic trees.

Each tree is represented by a valid parenthesis-expression. Each internal vertex $u$ of the tree is represented by the expression $(E_1,E_2,\ldots,E_d)$ where each $E_i$ is an expression for the subtree rooted at the $i$’th child of $u$. Each leaf of the tree is represented by its label. The whole expression is terminated with a semi-colon.

The two trees above can be represented as follows:

(((E,F),(C,D)),(A,B));
(((((D,B),A),E),C),F);

Output Format

The output format is the same as the input format, but consisting of $k$ phylogenetic trees whose leaf-labels are a partition of the leaf-labels of each input tree.

The solution for the example above could be the following:

(F,E);
D;
C;
(A,B);

Literature